In real social life, each of us has observed how the third persons affect the relationship between two persons. It means the relationship between two persons is only depended on them, but also it is interested in by others. The relationships are balanced if two persons, who are friends, have the same attitude (friendly or unfriendly) toward a third one, otherwise in order to decrease tension, one of them must change his or her attitude or they have to stop their friendship. This concept was introduced for the first time by Heider (1946) in the framework of the balance theory. His sentence is a key in Balance theory: “We adjust our relationship based on reducing the psychological stresses”. If a person’s beliefs are unbalanced, psychological stresses will generate internal pressures to change either some of the sentiments (liking, disliking) or some relationships (proximity, membership) into a more congruent pattern.
Cartwright and Harary (1950) introduced the psychological stresses by defining a triple as unbalanced if the product of its edge signs is negative. They said everybody can sense the psychological stresses of a person that loves her/his parents and partner when they cannot accept each other. Now, this is how it goes; the relation (link) between the members (nodes) i and j is represented by Sij, where if i and j are equal. If the status between two nodes is friendship/enemy, we would have for Sij the values of 1 and −1, respectively. This imposes that for a three node system which shapes a triangle, a balanced triangle is formed only when the product of the values assigned for the links (Sij) between every two nodes has a positive sign. Hence, we would have two balanced and two unbalanced states. Note that the tendency is to have a balanced triangle, which implies that as the network evolves, the unbalanced triangles eventually become balanced.
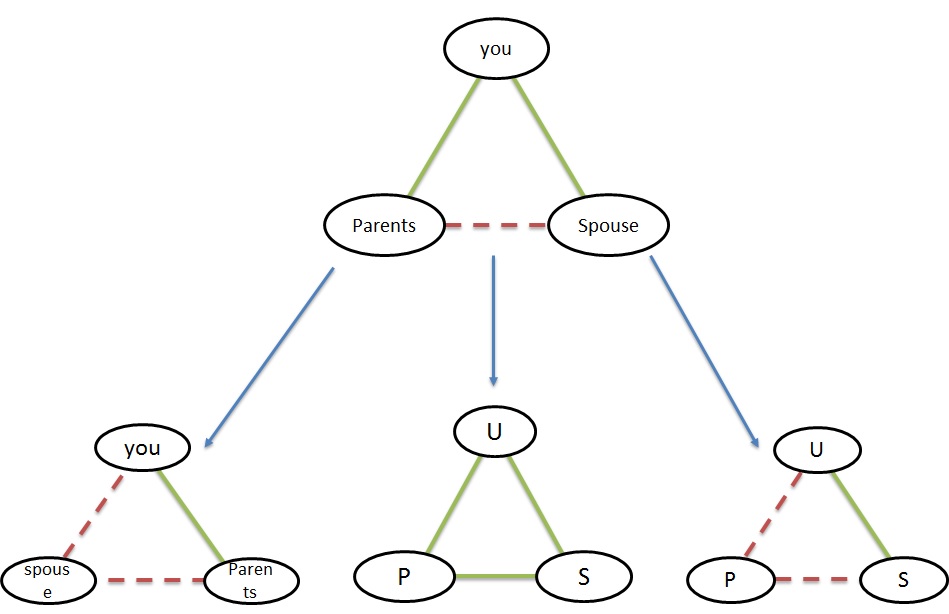
But the problem is that we are not living in a single triplet.
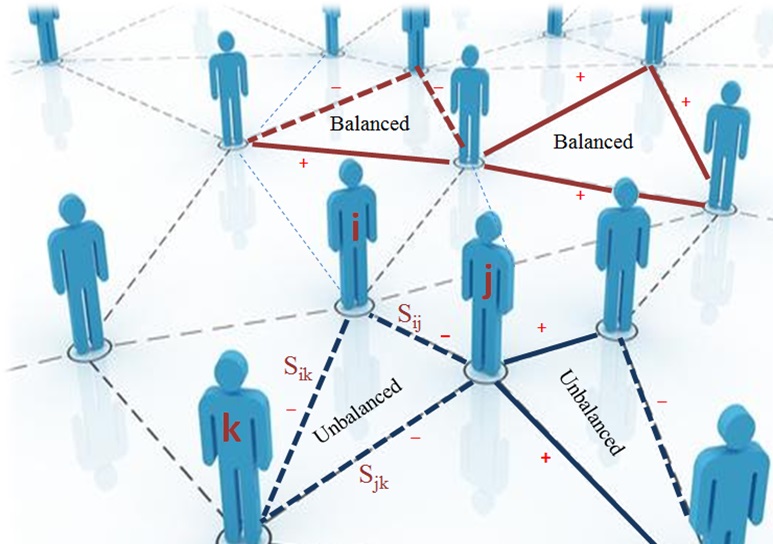
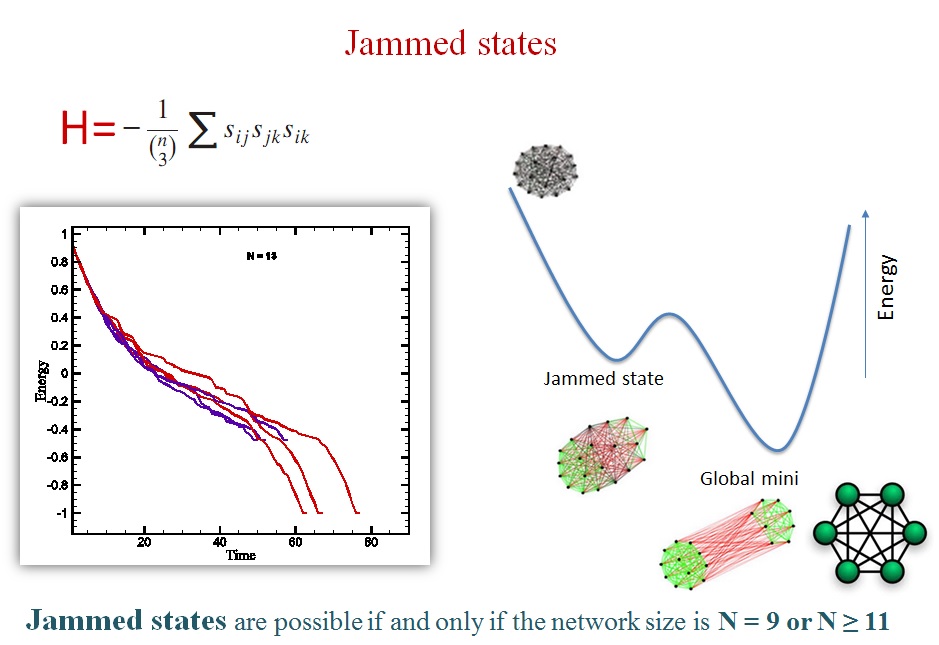
However, in the case of a weighted network where not all the nodes are connected to each other, Estrada & Benzi provided a method for measuring how balanced the situation is. Since the balanced and unbalanced states for the triangles are respectively referred to as the negative and positive energies, a Hamiltonian definition for these triangles is provided
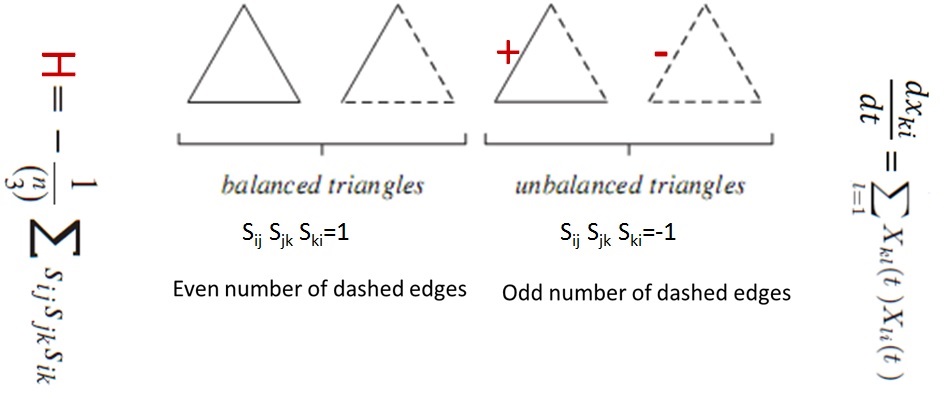
where n is the size of the network. Note that the energy is obtained by subtracting the number of unbalanced triangles from the number of balanced triangles and normalizing to the total number of triangles. Hence, the Hamiltonian obtains values only between −1 and +1. By having in hand the Hamiltonian of a system together with the trend in which the energy is reducing, a model for its dynamics could be provided.
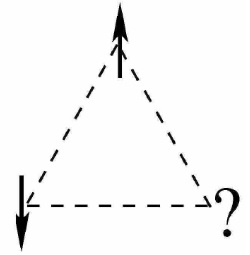
In the triplet relationship, an important point is
Refs
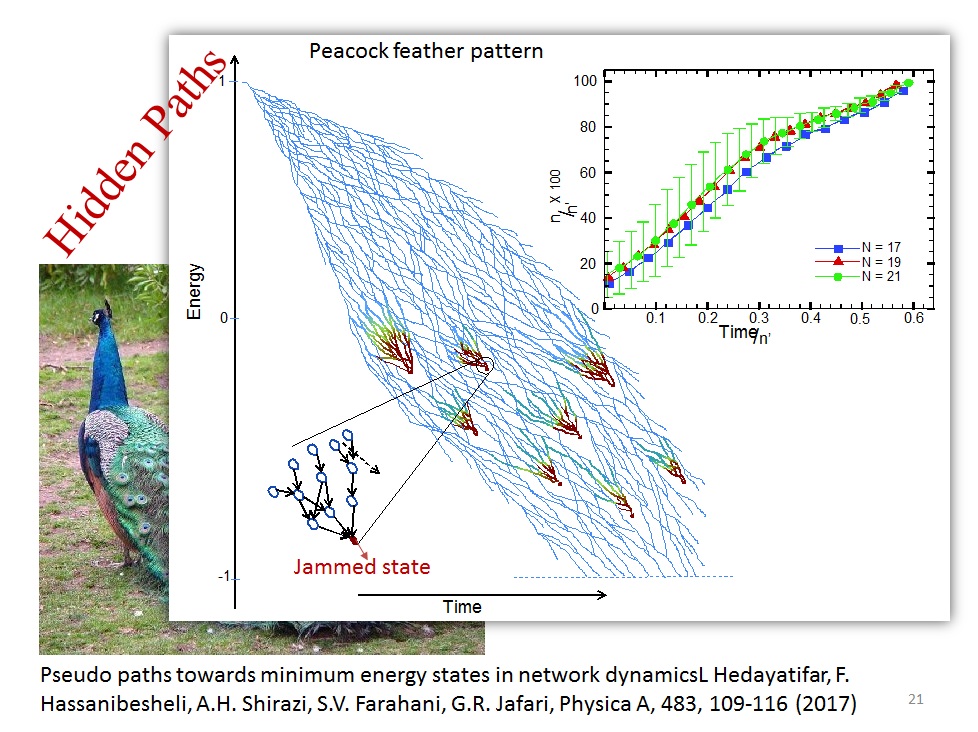
- Pseudo paths towards minimum energy states in network dynamics, L Hedayatifar, F Hassanibesheli, AH Shirazi, SV Farahani, GR Jafari, Physica A: Statistical Mechanics and its Applications 483, 109-116 (2017)
- Epidemic spreading on evolving signed networks, M. Saeedian, N. Azimi-Tafreshi, G. R. Jafari, J. Kertesz, Physical Review E 95, 022314 (2017)
- Glassy states of aging social networks, F Hassanibesheli, L Hedayatifar, H Safdari, M Ausloos, GR Jafari, Entropy 19 (6), 246 (2017)